LES POINTS DE LAGRANGE  
par Jean Pierre MARTIN                 http://www.planetastronomy.com

DES RAPPELS DE PHYSIQUE INDISPENSABLES
Soit un système où un corps tourne autour d'un autre beaucoup plus gros (par exemple, la Terre autour du Soleil ou la Lune autour de la terre etc..), on s'aperçoit qu'il existe 5 positions dans cet ensemble où un troisième corps (un satellite, des astéroïdes, etc..) peut résider de façon fixe stable ou instable. Pour calculer ces points nous avons besoin de quelques rappels mathématiques et physiques :

* GRAVITÉ, LOI D'ATTRACTION UNIVERSELLE

Deux corps situés à une distance d l'un de l'autre sont attirés par une Force F qui est proportionnelle à leurs masses et inversement proportionnelle au carré de leur distance. C'est une force UNIVERSELLE, qui ne peut pas être annulée ni masquée et qui agit à distance. À chaque instant nous attirons par exemple l'étoile Véga et elle nous attire de la même valeur, bien entendu le fait que le carré de la distance intervienne, fait que plus les corps sont proches, plus les forces sont à prendre en compte. On peut écrire cette formule de la façon suivante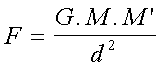
Avec : M et M' les masses respectives et d la distance. G est une constante appelée constante de la gravitation universelle elle vaut : 6,67 10^-11 Nm²kg^-2

* LOIS DE LA MÉCANIQUE DE NEWTON :
Première Loi : En l'absence de Forces agissant sur lui, tout corps est soit au repos soit se déplace à vitesse constante en ligne droite.
Deuxième Loi : Quand une force est appliquée à un corps, il s'accélère dans la même direction et cette accélération est proportionnelle à la Force et inversement proportionnelle à sa masse :
Rappel : sur Terre Γ est égale à g (accélération de la pesanteur) = 9,8 m/s/s
Troisième Loi : Toute action entraîne une réaction égale et opposée.

* FORCE CENTRIFUGE/CENTRIPÈTE : mouvement circulaire

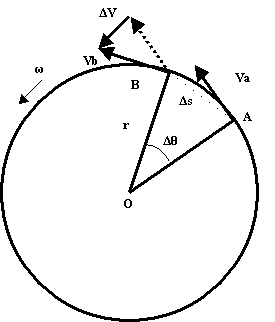
Soit un mobile (une planète, un satellite) se déplaçant sur un cercle de centre O (le soleil ou la Terre par exemple), par définition l'arc de cercle s parcouru est lié au Rayon r et à l'angle intercepté θ par la relation :
s = r. θ avec θ en RADIANS,
(par extension, pour θ=2Π on a : longueur de la circonférence = 2 Πr)
Par définition, la vitesse tangentielle du mobile sur sa trajectoire est
vitesse = dérivée du déplacement par rapport au temps :
v = Δs/ Δt
mais sachant que s est lié à l'angle θ , on a :
Δs = r Δθ
On obtient v= r Δθ/ Δt or à la limite, quand Δt tend vers 0, le rapport représente la VITESSE ANGULAIRE ω du mobile (en Rd/sec), d'où la formule liant la vitesse angulaire ω à la vitesse tangentielle par la formule :

v = r ω

Vous avez tous compris que la vitesse angulaire correspondait soit à la période de rotation d'une planète soit d'un satellite, sauf qu'elle est exprimée avec différentes unités.
Revenons à notre mobile (notre planète), ce point tourne par exemple à vitesse ANGULAIRE constante (mais le vecteur vitesse, constant en valeur absolue, ne l'est pas en direction, sa direction change à tout moment), ce point pour rester sur sa trajectoire est donc soumis à une ACCÉLÉRATION (sinon 1^ère loi de Newton, il s'en irait en ligne droite), calculons cette accélération qui est forcément dirigée vers le centre (centripète) :

Le triangle formé par les vecteurs vitesse en A et B et Δv et le triangle formé par O , A et B sont semblables et isocèles évidemment, donc on peut dire que (Thalès) :


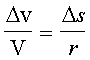
Or par définition, l'accélération est la dérivée de la vitesse et est perpendiculaire au vecteur vitesse soit

Γ = Δv/Δt
En remplaçant Δv par sa valeur, l'accélération est donnée par la formule:

on reconnaît la valeur de v dans Δs/Δt et la formule de l'accélération centripète devient :

Γ = v²/r = ω² r

Le mobile est donc soumis à une force (2^ème loi de Newton) F telle que F = m Γ soit :

F = m v²/r = mω²r

Bon nous avons tous les outils maintenant pour étudier les points de Lagrange.

LES POINTS DE LAGRANGE CALCUL
CE NE SONT PAS COMME ON CROIT LES POINTS OU L'ATTRACTION D'UN CORPS (SOLEIL PAR EXEMPLE) CONTREBALANCE L'ATTRACTION DE L'AUTRE (TERRE PAR EXEMPLE), car on ne peut pas rester ainsi dans l'espace sans "bouger", tout corps est soumis à des forces et se trouve donc sur une trajectoire autour du soleil (dans notre système solaire), il est donc AUSSI SOUMIS À UNE FORCE CENTRIFUGE.
Si l'on considère deux corps de très grande masse (Terre et Soleil par exemple), il existe des positions privilégiées pour un troisième corps de masse négligeable (d'où le nom de problème de trois corps, three body problem en anglais).
Ces points découverts par notre ami Lagrange, sont des points qui tournent donc à la MÊME VITESSE QUE LE CORPS TOURNANT AUTOUR DU CORPS CENTRAL (La terre par exemple), et qui sont FIXES par rapport à cet ensemble
Seulement il y a un problème, les lois de la mécanique céleste (lois de Kepler) imposent la période de rotation quand on est à une certaine distance du centre (soleil), c'est la fameuse loi T²/a³ = constante. Donc un corps (satellite, astéroïde..) ne pourrait pas se trouver sur une orbite différente de la Terre par exemple et avoir une période de 1 an. Et bien ce n'est pas tout à fait exact, c'est ce que Lagrange a prouvé. (voir dessin)

En effet si ce petit corps est situé suffisamment près de la Terre, l'attraction terrestre contrebalance en partie l'attraction du soleil et il lui faut moins de vitesse pour rester sur une orbite qui fait un an de période, donc synchrone avec la terre..
Les points de Lagrange sont donc les points où l'ATTRACTION SOLAIRE ET L'ATTRACTION TERRESTRE SONT EXACTEMENT COMPENSÉES PAR LA FORCE CENTRIFUGE SUR ORBITE.
CES POINTS SONT DONC FIXES PAR RAPPORT A L'ENSEMBLE M (Soleil par exemple) ET m (Terre par exemple), les dénominations L1 à L5 sont classiques..
Les points de Lagrange sont donc des endroits dans l'espace où un troisième corps comme un satellite peut rester fixe par rapport aux deux autres, ces points sont importants car ils nécessitent souvent peu de carburant pour rester en place (les corrections de trajectoires sont minimes). De tous ces points, il y en a 5 en tout, seuls L4 et L5 sont stables, ce qui veut dire que la matière a tendance à s'accumuler à ces endroits. Les autres sont instables, c'est à dire qu'il faut très peu de chose pour qu'ils s'éloignent de ces positions.

(d'après cours astro Nasa du Goddard Spaceflight Center)

POINTS DE LAGRANGE

MÉNAGE À TROIS

Le satellite SOHO est au point L1 du système Soleil-Terre, essayons de déterminer sa position.
Quelles sont les forces agissant sur un corps situé en L1 :
*** Attraction du Soleil Fs
*** Attraction de la Terre Ft
*** Force centrifuge autour du soleil Fc'
on a en ce point L1 : (ce qui éloigne : Fc et Ft, ce qui attire Fs)
Fs = Fc + Ft
avec M= masse soleil m= masse terre μ= masse (petite) satellite R = rayon orbite terre = 1UA et r = distance de L1 à la Terre (<< R), nous avons donc d'après précédemment :

et

Nous avons donc en simplifiant :
or en ce point la période de rotation T est ÉGALE à celle de la Terre (1 an) puisque fixe par rapport à celle-ci, mais si on considère la Terre seule, elle est en équilibre entre l'attraction solaire et la force centrifuge de la terre sur son orbite, on peut donc écrire, si T est aussi la période de rotation de la terre (1 an) :

on peut donc en remplaçant dans la formule plus haut :

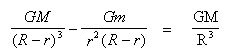posons pour simplifier : y = m/M (très petit) et z= r/R (petit)

et en sachant que 1/(1-z)³ ~ 1 + 3z l'équation se simplifie puissamment en :


3 z³ = y soit : 3 (r/R)³ = m/M
Dans le cas du système Terre-Soleil :

Le soleil est 330.000 fois plus lourd que la Terre (m/M = 3 10^-6, on en déduit que le rapport r/R vaut approximativement : 1% soit la distance r du point de Lagrange L1 de la terre est à 1% de la distance Terre-Soleil soit r = 1,5 Million de Km de la Terre

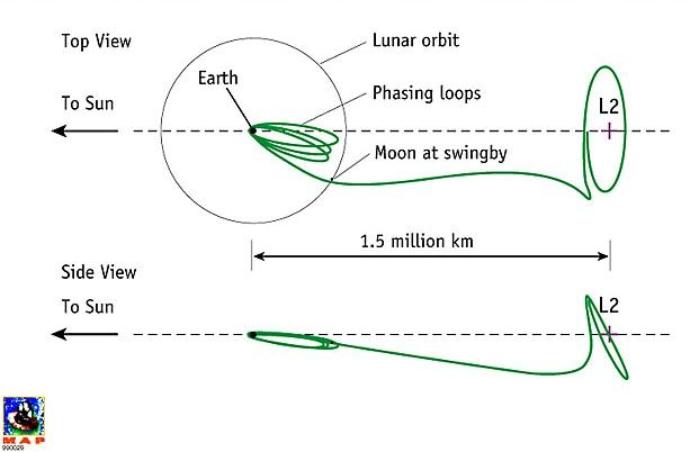
On pourrait aussi calculer la distance de L2 (où Fs = Ft + Fc) qui est symétrique par rapport à m (la Terre) donc aussi à 1,5 Mkm de celle-ci, Tiens puisque l'on parle de L2, il ne vous a pas échappé que le satellite WMAP (Wilkinson Microwave Anisotropic Probe) lancé le 30 Juin 2001 va se mettre en orbite autour de L2 afin d'être le moins perturbé, ce sera aussi le cas du télescope spatial remplaçant Hubble. On peut aussi calculer les autres positions.
On s'aperçoit que les seuls points stables L4 et L5 sont à 60 degrés en avant et en arrière de l'orbite de la Terre (où il y a d'ailleurs un amas d'astéroïdes)

(NASA-ESA)

SOHO AND THE TWIN COMETS IN 1998 (ESA-NASA)

AUTRES EXEMPLES DANS LE SYSTÈME SOLAIRE

Mais il y a des exemples "naturels" dans le système solaire, il y a des endroits où des astéroïdes s'amassent donc en position stable c'est à dire en L4 et L5. Voyons voir lesquels.
Le premier exemple qui vient à l'esprit est Jupiter, en effet c'est la plus grande planète de notre système, elle doit donc jouer un certain rôle dans ces histoires d'équilibre d'attractions. En effet sur l'orbite de Jupiter on trouve à L4 et L5 (60degré en avant et en arrière) les astéroïdes appelés les "Troyens". De même aux même points du système terre-lune-soleil en L4 et L5 on a détecté une anomalie de concentration en astéroïdes.
On a découvert aussi un "Troyen" pour Mars : l'astéroïde 5261 Eureka; Saturne possède de nombreux satellites (30) dont Dione et 60 degrés en avant de Dione il y a un petit bout de roche qui s'appelle Hélène ,etc..
On pourrait trouver des amas de matières à tous les points de Lagrange stables des plus importantes planètes et aussi des systèmes solaires et galaxies. Si on en n'a pas trouvé encore c'est que la résolution des instruments n'est pas suffisante.

MAIS QUI ÉTAIT DONC CE MONSIEUR LAGRANGE ???

Et d'abord qui était ce Sieur Joseph-Louis Lagrange, né en 1736 et mort en 1813, et qui survécut donc à la Révolution Française. N'en déplaise aux Français, c'était un Italien, né à Turin (Guiseppe Lodovico Lagrangia) d'une famille modeste de Savoie, très jeune il s'intéressait aux œuvres de Halley et eut beaucoup de contacts avec le mathématicien Allemand Euler, qui lui proposa d'ailleurs un poste à Berlin, et à l'age de 20 ans (!) Il est élu à l'Académie de Berlin, puis devint membre de l'Académie des Sciences de Turin. Lagrange, oui car il préférait se faire appeler par la version française de son nom, concourt à l'Académie des Sciences de Paris en soumettant sa réponse au problème posé concernant les librations de la Lune. Il est toujours à Berlin où il remplace Euler à la chaire de mathématiques à l'age de 30 ans. Il fait ses plus grandes découvertes mathématiques à Berlin qui vont s'avérer fondamentales pour cette discipline. Plus âgé (50 ans) il accepte l'offre de Paris et devient membre de l'Académie des Sciences juste avant la Révolution. Pendant cette période trouble qu'est la Révolution, tout semble bloqué au point de vue scientifique, tout… et bien non, pas tout, la Révolution veut faire don au monde du système métrique et Lagrange devient le responsable de la commission du système métrique et du système décimal. Il survit pendant la Révolution à la chasse aux étrangers (il est italien) et il est sauvé en fait par notre célèbre Lavoisier; il ne peut malheureusement pas lui rendre la monnaie de sa pièce, Lavoisier est condamné à mort quelques temps après par des révolutionnaires ignares.
Il devient professeur d'analyse à l'École Polytechnique nouvellement créée. C'est lui qui introduit les termes "primitive" et "dérivée" qui seront employés dans le calcul intégral de façon générale. Napoléon le fait chevalier de la Légion d'Honneur en 1808.
Pendant sa très longue et européenne carrière, il s'est amusé à essayer de résoudre les problèmes de trois corps qui s'attirent (au sens de Newton bien sur!) même si il n’a pas découvert lui même ces fameux points qui portent son nom.
Voyons donc cela maintenant.

BIBLIOGRAPHIE ET SITES WEB

Bibliographie :

· N'importe quel livre de physique de Terminale ou de Math Sup

· L'astronomie populaire de C. Flammarion (oui je sais ce n'est pas jeune, moi non plus!)

· Astronomie Générale de Bakouline et coll. aux Editions de Moscou : un classique même si vous n'avez pas été au goulag.

· Exploration of the Solar System par W.J. Kaufmann Mac Millan New York

· The story of Physics chez Avon Books New York : l'histoire de la physique et des physiciens en livre de poche

Web sites (en anglais) :

· http://www-spof.gsfc.nasa.gov/stargaze/Slagrang.htm : Le plus complet : de mon ami David Stern de la NASA au Goddard Space Flight Center dans son cours d'Astro

· http://solar-center.stanford.edu/FAQ/QL1.html : de la Stanford University. Théorique

· http://www.merlyn.demon.co.uk/gravity0.htm : très théorique et très complet sur gravité et attraction (Lagrange, limite de Roche etc..)

· http://sohowww.nascom.nasa.gov : sur le satellite SOHO

modifié/complété Oct 2012