
Mise à jour 13 Septembre 2015
CONFÉRENCE MENSUELLE DE LA SAF
«L’ESPACE-TEMPS, CENT ANS DE RELATIVITÉ»
Par Marc LACHIÈZE-REY
Dr de rech. CNRS Astrophysicien APC (Astro Particules et Cosmologie)
À l’AgroParisTech 16 rue C Bernard Paris 5.
Le Mercredi 9 Septembre 2015 à 19H00 Amphi Tisserand
Photos : JPM pour l'ambiance (les photos avec plus de résolution peuvent m'être demandées directement)
Les photos des slides sont de la présentation de l'auteur. Voir les crédits des autres photos et des animations.
Le conférencier a eu la gentillesse de nous donner sa présentation, elle est disponible sur ma liaison ftp et s'appelle :
.pdf, elle est dans le dossier CONF-MENSUELLES-SAF/ saison 2014-2015. .
Ceux qui n'ont pas les mots de passe doivent me contacter avant.
Cette conférence a été filmée en vidéo (grâce à UNICNAM et IDF TV) et est accessible sur Internet
On la trouve à cette adresse disponible dans quelques jours

Salle pleine pour notre célèbre cosmologiste

Marc Lachièze-Rey est un de nos plus grands astrophysiciens, il travaille au centre APC, Astro Particules et Cosmologie qui dépend de l’Université Paris VII.
Il a publié de nombreux ouvrages à la fois très spécialisés mais aussi certains, plus à la portée du grand public. Voir en bas de ce compte rendu.
Il nous parle (toujours sans notes) de l’évolution des notions d’espace et de temps dans la physique et comment Albert Einstein a révolutionné notre vie en cette année du centenaire de la découverte du principe de la théorie générale de la Relativité.
AVANT EINSTEIN.
C’est la physique de Newton qui mène la danse. La gravitation est une interaction qui s’exprime par une force.
Le principe d’inertie dirige le monde : tout corps (dans un référentiel galiléen) en l’absence d’influence extérieure continue à vitesse constante son mouvement rectiligne uniforme.
Newton explique parfaitement comment un corps massif peut exercer une action à distance sur un autre corps, cela conduira plus tard à la découverte de Neptune par le calcul.
Il y avait une exception dans le système solaire, c’était Mercure, seul problème de la physique newtonienne, l’avance de son périhélie ne pouvait pas être expliquée. Il faudra attendre Einstein.
LA DÉMARCHE D’EINSTEIN.
Einstein réfléchit à la théorie de Newton, où espace et temps sont séparés. Chez Newton l’espace est absolu.
Concernant le temps, Newton l’assimile à une droite. À chaque instant on peut définir la durée par rapport à une origine.
La propriété essentielle du temps newtonien est que l’on peut associer une date à n’importe quel événement.
 De plus l’interaction à distance (comme l’effet de la gravitation) sans contact semble magique. C’est pour cela que Newton avait inventé l’éther qui permettait le transport de cette interaction.
De plus l’interaction à distance (comme l’effet de la gravitation) sans contact semble magique. C’est pour cela que Newton avait inventé l’éther qui permettait le transport de cette interaction.
La physique de Newton permet aussi la loi de composition des vitesses, mais cela ne marche plus avec la constance de la vitesse de la lumière (la vitesse de la lumière est la même dans tous les repères), il faudra étendre cette loi en en tenant compte.
On a bien essayé de mettre en défaut cette constance mais sans succès : voir l’expérience de Michelson et Morley.
Poincaré et Lorentz essaie aussi de résoudre le problème de la composition des vitesses et cela aboutit vers les années 1920, aux célèbres transformations de Lorentz, qui se réduisent aux formules newtoniennes dans la vie de tous les jours.
Albert Einstein, en 1905, publie, au travers d’une série d’articles, sa théorie de la Relativité Restreinte , restreinte car sans gravitation, en anglais special relativity) où il n’y a pas d’espace ni de temps, il n’y a que
l’espace-temps, qui est différent de la simple réunion de l’espace et du temps !
Cette théorie nous sert tous les jours avec le GPS par exemple!!
Quand la vitesse d'un objet est proche de celle de la lumière, il se passe des phénomènes qui vont contre le sens commun :
· Le temps ralentit
· Les distances se contractent
· La masse des objets augmente.
Elle est aussi la base du paradoxe des jumeaux de Langevin.
 On considère deux jumeaux, l’un fait un voyage dans l’espace à une vitesse proche de la vitesse de la lumière et revient sur Terre, l’autre reste sur Terre. Au départ disons qu’ils ont 20 ans tous les deux. Au retour sur Terre, le jumeau resté sur Terre a 40 ans, le jumeau astronaute 30 ans !
On considère deux jumeaux, l’un fait un voyage dans l’espace à une vitesse proche de la vitesse de la lumière et revient sur Terre, l’autre reste sur Terre. Au départ disons qu’ils ont 20 ans tous les deux. Au retour sur Terre, le jumeau resté sur Terre a 40 ans, le jumeau astronaute 30 ans !
Il y a eu dilatation du temps. Pour le jumeau resté sur Terre, la durée de l’absence de son frère est supérieure au temps passé par celui qui voyage.
Mais contrairement à ce que l’on pourrait croire, ils ont vécu pendant le voyage, chacun réellement 20 ans et 10 ans biologiques que l’on peut vérifier aussi sur une montre.
C’est la preuve que le temps n’existe pas !
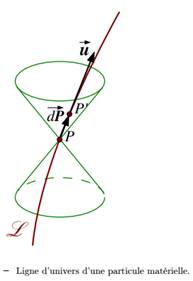
C’est une nouvelle manière de voir les choses : Einstein a beaucoup réfléchi à la notion de temps et de simultanéité, il postule que la simultanéité n’est pas absolue, chacun possède ce qu’il va appeler son temps propre, le temps n’est plus le même que celui de Newton.
Chacun va décrire sa « ligne d’Univers » c’est-à-dire son itinéraire personnel dans l’espace-temps.
La longueur de cette ligne d’Univers est sa durée propre ou son temps propre.
Dessin tiré du cours d’E. Gourgoulhon.
VERS LA RELATIVITÉ GÉNÉRALE.
En 1905, cette théorie est révolutionnaire, mais Einstein n’est pas satisfait, la gravitation ne fait pas partie de sa théorie.
Il veut absolument inclure la gravitation dans celle-ci.
Pour cela il doit utiliser des mathématiques un peu spéciales : la géométrie riemannienne.
Cela nous mène à la notion de variété :
Extraits de Géométrie différentielle, variétés, topologie différentielle de Serge Mehl.
Suite aux travaux novateurs de Gauss dans l'étude des surfaces, Riemann développa ce qui devint une branche maîtresse des mathématiques : la géométrie différentielle.
L'objectif fut de généraliser les propriétés métriques et différentielles des surfaces "usuelles" de l'espace euclidien à des espaces "courbés" considérés comme espaces de référence et non plus comme plongés dans un espace plus vaste de dimension supérieure : on parle de variétés.
Une courbe plane ou gauche est une variété de dimension 1.
La sphère ou le paraboloïde hyperbolique (en forme de selle de cheval, à droite) sont des variétés de dimension 2.

Dessin tiré du cours d’E. Gourgoulhon
Une variété est dite algébrique si elle admet une équation polynomiale du type f(x,y,z,...) = 0. Une conique, un cercle sont des variétés algébriques de dimension 1, la sphère est une variété algébrique de dimension 2 (surface).
On définit aujourd'hui abstraitement une variété topologique de dimension n comme un espace topologique connexe séparé localement homéomorphe (homéomorphisme = bijection continue ainsi que sa réciproque) à un ouvert de Rn : chaque point de admet un voisinage ouvert homéomorphe à un ouvert de Rn. On parle de variété topologique de
dimension n. Le très important et vaste sujet des variétés de dimension 2 est l'étude des surfaces.
Par exemple, à vue de nez, sur Terre, en chaque point de sa surface S, votre voisinage est homéomorphe localement à une "boule" de R2, en l'occurrence un disque (dimension 2), c'est à dire quelque chose de plat. Ce disque est pour vous une carte (locale) en x. Si l'ensemble de vos cartes recouvre S, elles constituent un atlas dont l'étude permet de rendre compte des propriétés de la
variété.
Si une variété est étudiée en tant que sous-espace ("plongé" dans un espace qui la contient), elle peut être limitée et posséder des points frontières qui vont en constituer le bord et la définition donnée au départ selon laquelle chaque point de admet un voisinage ouvert homéomorphe à un ouvert de Rn ne convient alors plus car tout
voisinage d'un point frontière déborde dans l'espace environnant. On convient de distinguer trois types de variétés topologiques :
·
les variétés closes : compactes, au sens topologique de fermées et bornées, comme la sphère ou le tore qui sont des variétés de dimension 2. Elles n'ont, concrètement, pas de bord ou d'extrémité. La définition donnée convient.
·
les variétés ouvertes : entrent dans cette catégorie les variétés non compactes, comme certains ouverts de Rn, par exemple, dans R : l'intervalle ]-1,1[ de dimension 1, dans R2 : le disque x²+y² < 1 de dimension 2, dans R3 : la boule unité ouverte x²+y²+z² <1, de dimension 3. Une telle variété n'a pas de bord au sens mathématique car il est réservé à
des variétés fermées. La définition donnée convient là encore.
·
les variétés à bord : le bord (ou frontière) d'une variété fermée (au sens topologique) est l'ensemble de ses points frontières également dits points bordants. Comme dit ci-dessus, on les reconnaît concrètement par le fait que tout voisinage d'un point frontière déborde dans l'espace environnant contrairement aux surfaces closes où tout voisinage de tout point y est entièrement inclus.
Einstein doit faire appel à des outils mathématiques complexes (géométrie riemannienne, calcul tensoriel et matriciel diverses métriques exotiques), qu’il ne maitrisait pas complètement bien, heureusement des amis mathématiciens (notamment Marcel Grossmann) lui firent profiter de leur expérience.
Et petit à petit il met au point la théorie générale de la relativité étendue à la gravitation, elle n’est donc plus restreinte.
Le cadre de cette nouvelle physique, c’est donc l’espace-temps, qui est défini comme une variété à 4 dimensions.
La gravitation va devenir une propriété de l’espace-temps qui introduit une courbure de cet espace-temps.
Les objets suivent la forme de l’espace-temps, ils suivent la courbure, leurs trajectoires ne sont plus des droites mais ce que l’on appelle des géodésiques, lignes de longueurs la plus courte.
La masse déforme l’espace-temps en créant une courbure de celui-ci.
Ce sont les équations d’Einstein qui vont permettre de calculer la courbure de l’espace-temps.
Dans le système solaire, le Soleil déforme l’espace-temps, il applique cette propriété à Mercure et ça marche.
Ses calculs expliquent l’écart de l’avance du périhélie de 43’’ d’arc par siècle, c’est la première preuve de l’exactitude de sa théorie.
Si la relativité restreinte a défini l’espace-temps, la relativité générale lui a donné une forme, une courbure liée à la gravitation.
La courbure est engendrée par l’énergie au travers de l’équation d’Einstein.
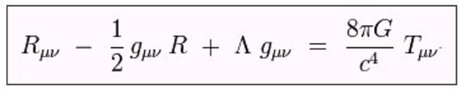
Cette équation lie la géométrie de l'espace-temps à la répartition de matière et d'énergie.
R est le tenseur de Ricci qui caractérise la courbure spatio-temporelle. T est le tenseur énergie-matière.
Ces équations sont valables dans tout l’Univers ; mais il est bien évident que dans notre système solaire (sauf Mercure), la physique newtonienne en découle pour tout ce qui est très inférieur à c et pour des masses relativement faibles.
LES VÉRIFICATIONS DE LA RELATIVITÉ GÉNÉRALE.
L’explication de l’avance du périhélie de Mercure est la première preuve de la justesse de la théorie d’Einstein, mais cela ne fait pas grand bruit.
C’est Eddington le grand astronome (et objecteur de conscience) britannique qui a l’idée de prouver la déviation des rayons lumineux par un objet massif, conséquence de la RG, lors d’une éclipse de Soleil.
 En 1919, doit se produire une éclipse totale de Soleil au Brésil et en Afrique notamment, c’est l’occasion inespérée de vérifier que le Soleil fait dévier les rayons lumineux d’objets situés derrière lui dans la ligne de visée, leurs positions
apparentes devaient être modifiées suivant qu’ils sont vus avec le Soleil (occulté de ses rayons aveuglants pendant l’éclipse) ou sans Soleil
En 1919, doit se produire une éclipse totale de Soleil au Brésil et en Afrique notamment, c’est l’occasion inespérée de vérifier que le Soleil fait dévier les rayons lumineux d’objets situés derrière lui dans la ligne de visée, leurs positions
apparentes devaient être modifiées suivant qu’ils sont vus avec le Soleil (occulté de ses rayons aveuglants pendant l’éclipse) ou sans Soleil
Deuxième succès pour la RG. Quelques jours après l’éclipse, le Times de Londres annonce la nouvelle : la lumière est tordue, la théorie d’Einstein triomphe ! Elle est maintenant vraiment reconnue.
Einstein devient une super star, immédiatement célèbre dans le monde entier.
Certains astronomes n’étant pas encore entièrement convaincus, répétèrent l’expérience lors de l’éclipse de 1922, il y eut confirmation des mesures de 1919.
Et c’est en 1960 qu’a lieu l’expérience de Robert Pound et Glen Rebka qui va vérifier aussi l’exactitude d’Einstein.
Ils eurent l’idée de mesurer le décalage de raies de 14,4keV émises par une source de Fe57 entre le bas et le haut d’une tour de 22m de Harvard. L’effet gravitationnel est minime (de l’ordre de 10-15), mais mesurable et plus direct que lors de l’expérience avec le Soleil. La
fréquence d’émission des atomes est modifiée par la gravitation. Cette expérience a été refaite avec des horloges atomiques situées en haut et en bas de la tour et a confirmé les précédents résultats.
La gravitation fait s’écouler le temps plus lentement, ce qui fait que les astronautes à bord de l’ISS (où la gravité est légèrement moins forte que sur Terre) paraissent vieillir plus vite que les terriens.
Einstein a vraiment gagné !
 C’est une révolution complète de la physique, mais personne ne va vraiment s’y intéresser, car la physique newtonienne est tellement plus simple. Même Einstein va délaisser sa nouvelle théorie et se tourner vers la physique quantique en publiant le fameux article sur
le paradoxe EPR (Einstein-Podolsky-Rosen).
C’est une révolution complète de la physique, mais personne ne va vraiment s’y intéresser, car la physique newtonienne est tellement plus simple. Même Einstein va délaisser sa nouvelle théorie et se tourner vers la physique quantique en publiant le fameux article sur
le paradoxe EPR (Einstein-Podolsky-Rosen).
C’était une expérience par la pensée afin de démontrer le caractère probabiliste de la mécanique quantique.
Photo : DP.
Il ne s‘intéressera de nouveau à sa théorie que plus tard, lorsque l’on parlera de plus en plus d’étoiles à neutrons et de trous noirs, objets célestes possédant un énorme champ magnétique et donc siège de phénomènes relativistes.
DEUX MONDES INCOMPATIBLES.
On est en présence de deux mondes, l’infiniment petit avec la Mécanique Quantique et son Modèle Standard, et l’infiniment grand avec la Relativité Générale et la gravitation.
Ces deux mondes sont incompatibles et s’ignorent, alors qu’indépendamment ils fonctionnent.
Ce sont deux langages différents. On sent bien qu’il manque quelque chose.
Une nouvelle physique est nécessaire. Einstein a passé la fin de sa vie à la chercher, mais sans succès.
On cherche toujours cette fameuse théorie du Tout.

Conclusion de cette superbe conférence avec de nombreuses questions.
POUR ALLER PLUS LOIN :
La relativité restreinte par astronomia.
Cours de relativité générale de Master 2 par Éric Gourgoulhon.
Le paradoxe EPR par Luxorion.
Einstein et les relativités : CR de la conf SAF (cosmo) de J Eisenstaedt du 17 Janv 2015
Vers la Gravitation Quantique : CR de la conférence SAF de M Lachièze Rey du 14 Janvier 2006
L'espace et le Temps : CR de la conférence IAP de M Lachièze Rey du 14 Mars 2006
"LE SIÈCLE D'ALBERT EINSTEIN" COLLOQUE DU 11 AU 15 JUILLET 2005 à l'UNESCO Paris
Quelques ouvrages écrits par M. Lachièze-Rey :
· Einstein à la plage chez Dunod
· Au delà de l'espace et du temps, Le Pommier 2004
· Les avatars du vide, Le Pommier 2005
· Initiation à la cosmologie chez Dunod
Bonne Rentrée à tous:
Prochaine conférence mensuelle de la SAF : Mercredi 14 Octobre 2015 19H00 AgroParistech Amphi Tisserand
Nous avons le plaisir de recevoir :
Marie Hélène SCHUNE Labo de l’Accélérateur Linéaire d’Orsay (LAL) Resp LHCb au LAL
Mais où est donc passée l’antimatière ??.
On sait qu'à l'origine, il y avait autant de matière que d'antimatière. Où est elle donc?
Est ce liée à la violation CP (Charge/Parité) pour certaines désintégrations?
C'est l'objet des recherches actuelles au CERN avec l'expérience LHCb
Entrée libre mais réservation obligatoire. À partir du 10 Sept.
Ce cycle 1915-2015 s'appelle : l'Odyssée de l'espace-temps.
Bon ciel à tous
Jean Pierre Martin Président de la commission de cosmologie de la SAF
Abonnez-vous gratuitement aux astronews du site en envoyant votre nom et e-mail.